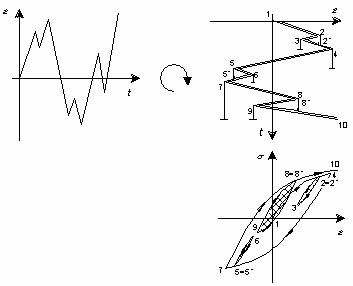
Load history decomposition

Load history decomposition is a procedure necessary for conversion of a “semi-continuous” load history record into a sequence of separate load cycles. The load cycles extracted are defined by upper and lower loads, where these loads can be described in one (uniaxial methods) or more dimensions (multiaxial analysis).

The most wide-spread and generally recognized method used for this extraction is the rain-flow method. The most of the current methods used even in the category of multiaxial loading are its clones performing the same decomposition process on some specific load component. Only the method defined by Wang & Brown in 1996 surpasses this concept and uses its own way.

Rain-flow

As regards the uniaxial methods, the generally accepted solution is the use of rain-flow counting procedure. The poetic name is related to inspiration of its inventors (Matsuishi & Endo [ME68]) by rain falling onto complex pagoda roofs. Here is a set of points that describe its algorithm as implemented in PragTic:

The rain runs out from different sources and streams down on the inclined roofs. There are two potential sources:

the start of the record (point 1),
the inward of each roof top (points 2, 3, 4, 5…).

The stream running down:

either goes into another stream falling from above – then it stops and a half-cycle is built (3-2’, 6-5’, 9-8’),
or it reaches the roof edge and falls over it down.

The stream falling down:

either reaches in some particular time instant:

a higher maximum then was the maximum, in which the stream originated,
a lower minimum then was the minimum, in which the stream originated

and a half-cycle is created. E.g. the stream originating in 2 ends on the level of point 4 like this.

Half-cycles of the same size and opposite direction close up a full cycle.

In order to quicken the calculation, Downing and Socie [DS82] proposed a two-pass algorithm, which follows the instructions above, but is based on a supreme pivotation. It requires that the full cycle is not closed if the half-cycle currently evaluated is higher than any preceding half-cycle. A rest of not closed half-cycles after the first pass can look like this:

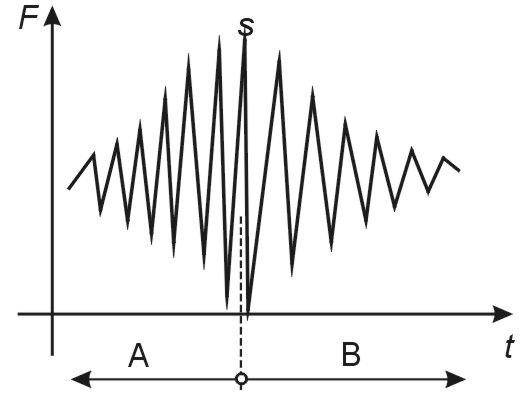
This is the case, in which is the option Close non-closed cycles in second run <1~yes, 0~no> in Calculation Methods dialogue important for the second pass. If the option 1 is chosen, all the time history in the part A is moved after the part B and the rain-flow procedure is run again. It is sure, that all cycles will be closed. The option 0 leads to an output of non-closed half-cycles, to which the weight should be assigned in Weight of non-closed half-cycles (probably 0.5).

It is clear that the closing of all half-cycles is a more conservative assumption if the weight is 0.5 or lesser. Nevertheless, if the weight is higher, than the unclosed variant is more detrimental.

There is one more option in Calculation Methods dialogue, which concerns the rain-flow counting. This is the size of eliminated cycles in Size of too small cycles (to be erased). If there is a lot of very small cycles, which do not have significant effect on the final damage, the computation of damage can become very slow due to the necessity to use Newton-Raphson iterative method for the most of the e-N curve based criteria. This option can speed-up the calculation.

Rain-flow multiaxial clones

There are clones of the basic rain-flow method, which operate not on an equivalent scalar load, but on loading on some specific plane. This is the case of e.g. the Socie method, where either normal or shear strain is decomposed with the rain-flow algorithm, while the history of second variable inside any closed half-cycle is related to it and evaluated inside it. See the texts on:

* Decomposition - rain-flow of resolved shear variable

* Decomposition - rain-flow of normal variable

More general multiaxial decomposition

Decomposition of load history into load cycles under multiaxial loading is relatively seldom solved. I (Jan Papuga, author) know only one more elaborated solution, which is the method proposed by Wang & Brown in 1996 [WB96]. Even here I cannot recall any later more extensive testing of validity of this method. The reason of the state of art is hidden above all in the fact, that there are too many effects in the multiaxial low-cycle fatigue, which interact in the numerical solution and which is relatively elaborate to eliminate in order to prove validity of some decomposition method.

The decomposition method of Wang & Brown is implemented in PragTic but it is currently accessible only for Wang & Brown fatigue life calculation method. For more reference on the method, please look onto:

* Decomposition - Wang & Brown v. 96

Calculation Methods dialogue

e-N curve

Socie method

Wang & Brown method

This help file has been generated by the freeware version of HelpNDoc